순환신경망 (1)

순환신경망

은닉층의 출력이 다시 은닉층의 입력으로 사용된다.
순환 구조라고 부르며 순환 구조가 있는 층을 순환층이라고 한다.

손실 함수에 대한 그레이디언트 : err_to_cell
W_1x, W_1h, b_1에 업데이트할 최종 그레이디언트는 err_to_cell과 각각의 도함수를 곱해서 구한다.

 

 순환신경망으로 텍스트 분류하기 

 

 

# 1.텐서플로에서 IMDB 데이터 세트 불러오기

import numpy as np from tensorflow.keras.datasets import imdb

▶load_data() 함수를 이용하여 데이터를 불러온다.

(x_train_all, y_train_all), (x_test, y_test) = imdb.load_data(skip_top=20, num_words=100) print(x_train_all.shape, y_train_all.shape) #훈련세트 크기확인

▶ skip_top : 가장 많이 등장한 단어들 중 건너뛸 단어의 개수를 지정(분석에 유용하지 않은)
num_words : 훈련에 사용할 단어의 개수를 지정

 

 

 

# 2.훈련샘플확인

print(x_train_all[0])

▶영단어가 아닌 정수 형태로 저장되어 있다.
영단어를 고유한 정수에 일대일 대응한 것이다. BoW(Bag of Word) 혹은 어휘 사전이라고 부른다.
가장 많이 등장하는 영단어 20개를 건너뛰고 100개의 단어만 선택
사전에 없는 영단어가 많을 수 있다.

 

 

 

# 3.숫자 2는 어휘 사전에 없는 단어 > 제외시키기

for i in range(len(x_train_all)):   x_train_all[i] = [w for w in x_train_all[i] if w > 2] print(x_train_all[0])

▶추가로 0과 1은 각각 패딩과 글의 시작을 나타내는 데 사용한다.

 

 

 

# 4.어휘사전 내려받기

word_to_index = imdb.get_word_index() word_to_index['movie']       #예를들어 movie라는 영단어는 17이라는 정수에 대응되어 있음

▶어휘 사전은 get_word_index() 함수로 내려받을 수 있다.
정수를 영단어로 바꾸려면 어휘사전을 내려받아 일대일로 다시 맵핑해야한다.

 

 

 

# 5.훈련세트의 정수를 영단어로 바꾸기

index_to_word = {word_to_index[k]: k for k in word_to_index}   for w in x_train_all[0]:   print(index_to_word[w - 3], end=' ')

▶3이상부터 영단어를 의미하므로 3을 뺀 값을 어휘 사전의 인덱스로 사용

 

 

#  6.훈련 샘플의 길이를 확인

print(len(x_train_all[0]), len(x_train_all[1]))

#59 32

▶훈련 세트의 입력 데이터는 넘파이 배열이 아니라 파이썬 리스트이다.
각 리뷰들의 길이가 달라 샘플의 길이가 다르다.
샘플의 길이가 다르면 모델을 제대로 훈련시킬 수 없다.

 

 

 

# 7.훈련세트의 타킷데이터확인

print(y_train_all[:10])

# [1 0 0 1 0 0 1 0 1 0]

▶1은 긍정 0은 부정을 의미

 

 

 

# 8.데이터 전처리

# 8-1)검증세트 준비 ;  permutation() 함수사용

np.random.seed(42) random_index = np.random.permutation(25000)   x_train = x_train_all[random_index[:20000]] y_train = y_train_all[random_index[:20000]] x_val = x_train_all[random_index[20000:]] y_val = y_train_all[random_index[20000:]]

▶25000개의 인덱스를 섞어 훈련,검증세트 분리
20000개 : 훈련세트, 나머지 : 검증세트

 

 

 

# 8-2)샘플길이 맞추기

from tensorflow.keras.preprocessing import sequence   maxlen=100 x_train_seq = sequence.pad_sequences(x_train, maxlen=maxlen) x_val_seq = sequence.pad_sequences(x_val, maxlen=maxlen)

▶일정 길이가 넘으면 샘플을 잘라버리고 길이가 모자라면 0으로 채우는 방식으로 길이를 조절

 

 

 

# 8-3) 샘플길이 맞춰 졌는지 확인

print(x_train_seq.shape, x_val_seq.shape)

# (20000, 100) (5000, 100)

 

print(x_train_seq[0])

▶샘플길이 변경한 훈련 세트의 첫 번째 샘플을 확인하면 왼쪽에 0이 채워져 있다.

 

 

# 9.샘플 원-핫 인코딩하기 ; to_categorical함수사용

from tensorflow.keras.utils import to_categorical   x_train_onehot = to_categorical(x_train_seq) x_val_onehot = to_categorical(x_val_seq)

print(x_train_onehot.shape)         # (20000, 100, 100) print(x_train_onehot.nbytes)        # 800000000

▶20000개의 샘플이 100차원으로 원-핫 인코딩됨

 

 

 

# 10.모델 만들기

import tensorflow as tf   class RecurrentNetwork:       def __init__(self, n_cells=10, batch_size=32, learning_rate=0.1):         self.n_cells = n_cells  # 셀 개수         self.batch_size = batch_size  # 배치 크기         """         w1h,w1x : 셀에 필요한 가중치         """         self.w1h = None  # 은닉 상태에 대한 가중치         self.w1x = None  # 입력에 대한 가중치         self.b1 = None  # 순환층의 절편         self.w2 = None  # 출력층의 가중치         self.b2 = None  # 출력층의 절편         """         h : 타임 스텝을 거슬러 그레이디언트를 전파하려면         순환층의 활성화 출력을 모두 가지고 있어야 하므로         """         self.h = None  # 순환층의 활성화 출력         self.losses = []  # 훈련 손실         self.val_losses = []  # 검증 손실         self.lr = learning_rate  # 학습률       def forpass(self, x):         """         각 타임 스텝의 은닉 상태를 저장하기 위한 변수 h를 초기화한다.         이때 은닉 상태의 크기는 (샘플 개수, 셀 개수)이다.         역전파 과정을 진행할 때 이전 타임 스텝의 은닉 상태를 사용.         첫 번째 타임 스텝의 이전 은닉 상태는 없으므로         변수 h의 첫 번째 요소에 0으로 채워진 배열을 추가.         """         self.h = [np.zeros((x.shape[0], self.n_cells))]  # 은닉 상태를 초기화합니다.         # 배치 차원과 타임 스텝 차원을 바꿉니다.         """         넘파이의 swapaxes() 함수를 사용하여         입력 x의 첫 번째 배치 차원과 두 번째 타입 스텝 차원을 바꾼다.         입력 x는 여러개의 샘플이 담긴 미니 배치이다.         정방향 계산을 할 때는 한 샘플의 모든 타입 스텝을 처리하고 그다음에 샘플을 처리하는 방식이 아니다.         미니 배치 안에 있는 모든 샘플의 첫 번째 타임 스텝을 한 번에 처리하고         두 번째 타입 스텝을 한 번에 처리해야 한다         """         seq = np.swapaxes(x, 0, 1)         # 순환 층의 선형 식을 계산합니다.         for x in seq:             z1 = np.dot(x, self.w1x) + np.dot(self.h[-1], self.w1h) + self.b1             h = np.tanh(z1)  # 활성화 함수를 적용합니다.             self.h.append(h)  # 역전파를 위해 은닉 상태 저장합니다.             z2 = np.dot(h, self.w2) + self.b2  # 출력층의 선형 식을 계산합니다.         return z2     """     모든 샘플의 타임 스텝을 한 번에 처리하기 위해 배치 차원과 타임 스텝 차원을 바꾼다.     """     def backprop(self, x, err):         m = len(x)  # 샘플 개수           # 출력층의 가중치와 절편에 대한 그래디언트를 계산합니다.         w2_grad = np.dot(self.h[-1].T, err) / m         b2_grad = np.sum(err) / m         # 배치 차원과 타임 스텝 차원을 바꿉니다.         seq = np.swapaxes(x, 0, 1)           w1h_grad = w1x_grad = b1_grad = 0         # 셀 직전까지 그래디언트를 계산합니다.         """         err_to_cell 변수에 저장되는 값 : Z_1에 대하여 손실 함수를 미분한 도함수의 결괏값         """         err_to_cell = np.dot(err, self.w2.T) * (1 - self.h[-1] ** 2)         # 모든 타임 스텝을 거슬러가면서 그래디언트를 전파합니다.         """         for문에서 슬라이싱 연산을 수행.         그레이디언트는 마지막 타임 스텝부터 거꾸로 적용해야 하므로 seq [::-1]을 사용         은닉 상태를 저장한 h 변수의 마지막 항목은         for문 이전에 err_to_cell 변수를 계산하기 위해 사용했기 때문에 이를 제외하고         self.h [:-1][::-1]와 같이 거꾸로 뒤집었다.         seq 넘파이 배열과 self.h 리스트를 거꾸로 뒤집은 다음         모든 타임 스텝을 거슬러 올라가지 않는다. 딱 10개의 타임 스텝만 거슬러 진행.         """         for x, h in zip(seq[::-1][:10], self.h[:-1][::-1][:10]):             w1h_grad += np.dot(h.T, err_to_cell)             w1x_grad += np.dot(x.T, err_to_cell)             b1_grad += np.sum(err_to_cell, axis=0)             # 이전 타임 스텝의 셀 직전까지 그래디언트를 계산합니다.             """             순환 신경망은 타임 스텝을 거슬러 올라가며 그레이디언트를 전파할 때 동일한 가중치를 반복적으로 곱한다.             이로 인해 그레이디언트가 너무 커지거나 작아지는 문제가 발생하기 쉽다.             이를 방지하기 위해 그레이디언트를 전파하는 타임 스텝의 수를 제한해야 한다-> TBPTT(Truncated Backpropagation Through Time)라고 한다.             W_1h의 그레이디언트(w1h_grad)를 구하기 위해 Z_1에 대한 손실 함수의 미분 값(err_to_cell)에 다음 식을 곱한다.             """             err_to_cell = np.dot(err_to_cell, self.w1h) * (1 - h ** 2)           w1h_grad /= m         w1x_grad /= m         b1_grad /= m           return w1h_grad, w1x_grad, b1_grad, w2_grad, b2_grad       def sigmoid(self, z):         z = np.clip(z, -100, None)  # 안전한 np.exp() 계산을 위해         a = 1 / (1 + np.exp(-z))  # 시그모이드 계산         return a     """     순환 신경망에서는 직교 행렬 초기화(orthgonal initialization)를 사용한다.     직교 행렬 초기화는 순환 셀에서 은닉 상태를 위한 가중치가 반복해서 곱해질 때     너무 커지거나 작아지지 않도록 만들어 준다.     """     def init_weights(self, n_features, n_classes):         """         가중치 초기화 클래스 : tensorflow.initializer모듈에 존재         직교 행렬 초기화 : Orthogonal클래스로 제공         """         orth_init = tf.initializers.Orthogonal()         glorot_init = tf.initializers.GlorotUniform()           self.w1h = orth_init((self.n_cells, self.n_cells)).numpy()  # (셀 개수, 셀 개수)         self.w1x = glorot_init((n_features, self.n_cells)).numpy()  # (특성 개수, 셀 개수)         self.b1 = np.zeros(self.n_cells)  # 은닉층의 크기         self.w2 = glorot_init((self.n_cells, n_classes)).numpy()  # (셀 개수, 클래스 개수)         self.b2 = np.zeros(n_classes)       def fit(self, x, y, epochs=100, x_val=None, y_val=None):         y = y.reshape(-1, 1)         y_val = y_val.reshape(-1, 1)         np.random.seed(42)         self.init_weights(x.shape[2], y.shape[1])  # 은닉층과 출력층의 가중치를 초기화합니다.         # epochs만큼 반복합니다.         for i in range(epochs):             print('에포크', i, end=' ')             # 제너레이터 함수에서 반환한 미니배치를 순환합니다.             batch_losses = []             for x_batch, y_batch in self.gen_batch(x, y):                 print('.', end='')                 a = self.training(x_batch, y_batch)                 # 안전한 로그 계산을 위해 클리핑합니다.                 a = np.clip(a, 1e-10, 1 - 1e-10)                 # 로그 손실과 규제 손실을 더하여 리스트에 추가합니다.                 loss = np.mean(-(y_batch * np.log(a) + (1 - y_batch) * np.log(1 - a)))                 batch_losses.append(loss)             print()             self.losses.append(np.mean(batch_losses))             # 검증 세트에 대한 손실을 계산합니다.             self.update_val_loss(x_val, y_val)       # 미니배치 제너레이터 함수     def gen_batch(self, x, y):         length = len(x)         bins = length // self.batch_size  # 미니배치 횟수         if length % self.batch_size:             bins += 1  # 나누어 떨어지지 않을 때         indexes = np.random.permutation(np.arange(len(x)))  # 인덱스를 섞습니다.         x = x[indexes]         y = y[indexes]         for i in range(bins):             start = self.batch_size * i             end = self.batch_size * (i + 1)             yield x[start:end], y[start:end]  # batch_size만큼 슬라이싱하여 반환합니다.       def training(self, x, y):         m = len(x)  # 샘플 개수를 저장합니다.         z = self.forpass(x)  # 정방향 계산을 수행합니다.         a = self.sigmoid(z)  # 활성화 함수를 적용합니다.         err = -(y - a)  # 오차를 계산합니다.         # 오차를 역전파하여 그래디언트를 계산합니다.         w1h_grad, w1x_grad, b1_grad, w2_grad, b2_grad = self.backprop(x, err)         # 셀의 가중치와 절편을 업데이트합니다.         self.w1h -= self.lr * w1h_grad         self.w1x -= self.lr * w1x_grad         self.b1 -= self.lr * b1_grad         # 출력층의 가중치와 절편을 업데이트합니다.         self.w2 -= self.lr * w2_grad         self.b2 -= self.lr * b2_grad         return a       def predict(self, x):         z = self.forpass(x)  # 정방향 계산을 수행합니다.         return z > 0  # 스텝 함수를 적용합니다.       def score(self, x, y):         # 예측과 타깃 열 벡터를 비교하여 True의 비율을 반환합니다.         return np.mean(self.predict(x) == y.reshape(-1, 1))       def update_val_loss(self, x_val, y_val):         z = self.forpass(x_val)  # 정방향 계산을 수행합니다.         a = self.sigmoid(z)  # 활성화 함수를 적용합니다.         a = np.clip(a, 1e-10, 1 - 1e-10)  # 출력 값을 클리핑합니다.         val_loss = np.mean(-(y_val * np.log(a) + (1 - y_val) * np.log(1 - a)))         self.val_losses.append(val_loss)

▶MinBatchNetwork 클래스를 기반으로 순환 신경망

 

 

# 11. 훈련 및 테스트

rn = RecurrentNetwork(n_cells=32, batch_size=32, learning_rate=0.01) rn.fit(x_train_onehot, y_train, epochs=20, x_val=x_val_onehot, y_val=y_val)

▶

 

 

# 12. plot(훈련, 검증 세트에 대한 손실 그래프)

import matplotlib.pyplot as plt plt.plot(rn.losses) plt.plot(rn.val_losses) plt.ylabel('rn.loss') plt.xlabel('epoch') plt.legend(['rn.losses', 'rn.val_losses']) plt.show()

▶비교적 손실이 잘 감소됨

 

 

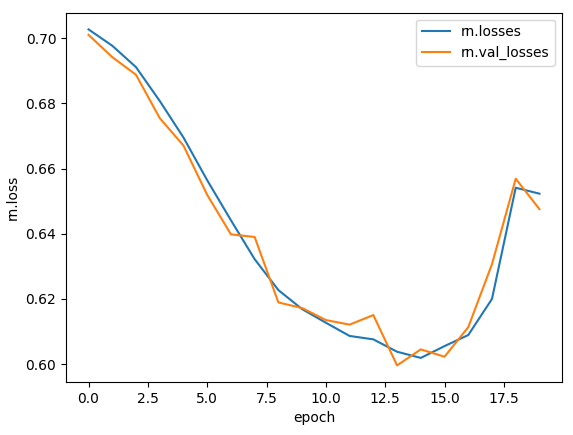
# 13 검증세트 정확도 평가하기

rn.score(x_val_onehot, y_val)

# 0.653

▶무작위로 예측하는 확률인 50% 보다는 좋은성능이지만 그렇게 좋은 성능은 아니다