[ R ] 집단간 차이분석 - 추정과 검정 #1
추정과 검정
(1) 점 추정과 구간 추청
- 점추정 : 하나의 값을 제시하여 모수의 참값을 추정하는 방법
- 구간추정 : 하한값과 상한값의 구간을 지정하여 모수의 참값을 추정하는 방법
(2) 모평균의 구간 추정
- 표본 평균이 따르는 분포 ~N(μ, σ 2 /n)
- 모표준편차 σ의 값이 알려지지 않는 경우 표본의 크기 n이 충분히 클 때 (n>= 30)는 표본표준편차 S 사용
신뢰도 모평균(μ)의 신뢰구간
95% : P(X − 1.96 𝜎 /√𝑛 ≤ 𝜇 ≤ X + 1.96 𝜎 /√𝑛 )
99% : P(X − 2.58 𝜎 /√𝑛 ≤ 𝜇 ≤ X + 2.58 𝜎 /√𝑛
ex) 우리나라 중학교 2학년 남학생의 평균 신장 표본조사
우리나라 중학교 2학년 남학생의 평균 신장 표본 조사를 위한 검정 통계량은 다음과 같다.
전체 표본 크기(N): 10,000명
표본 평균(X): 165.1cm
표본 표준편차(S): 2cm
| N <- 10000 X <- 165.1 S <- 2 low <- X-1.96*S/sqrt(N) high <- X+1.96*S/sqrt(N) low;high # [1] 165.0608 # [1] 165.1392 # 신뢰수준 95%의 모평균 신뢰구간: 165.0608 ≤ 𝜇 ≤ 165.1392 |
ex) 신뢰구간으로 표본오차 구하기
| high - X # [1] 0.0392 (low-X)*100 # [1] -3.92 (hing-X)*100 # [1] 3.92 |
(3) 모비율의 구간 추정
제품의 불량률 또는 대선 후보 지지율 등과 같이 모집단에서 어떤 사건에 대한 비율을 모비율(p)이라고 한다. 이러한 모비율 추정은 모집단으로부터 임의 추출한 표본에서 어떤 사건에 대한 비율을 표본 비율(p̂)이라고 하는데 이러한 표본비율을 이용하여 모비율을 추정할 수 있다
95% : P(𝑝̂− 1.96√ 𝑝̂𝑞̂ /𝑛 ≤ 𝑝 ≤ 𝑝̂+ 1.96√ 𝑝̂𝑞̂ /𝑛 )
99% : P(𝑝̂− 2.58√ 𝑝̂𝑞̂ /𝑛 ≤ 𝑝 ≤ 𝑝̂+ 2.58√ 𝑝̂𝑞̂ /𝑛
ex)--------------------------------------------------------------------------------------------------------------------------------------------------
N=150
𝑝̂ = 90/150 = 0.6
전체 사원 중 여자사원의 비율 p의 신뢰도 95% 신뢰구간은
P(0.6 − 1.96√ 0.6 × 0.4 /150 ≤ 𝑝 ≤ 0.6 + 1.96√ 0.6 × 0.4 /150 )
0.5216 ≤ 𝑝 ≤ 0.6784
-------------------------------------------------------------------------------------------------------------------------------------------------------
단일 집단 검정
한 개의 집단과 기존 집단과의 비율 차이 검정과 평균 차이 검정
비율차이 검정: 빈도수에 대한 비율에 의미
평균 차이 검정: 표본 평균에 의미
(1) 단일집단 비율 검정
ex)--------------------------------------------------------------------------------------------------------------------------------------------------
귀무가설(H0): 기존 2019년도 고객 불만율과 2020년도 CS교육 후 불만율에 차이가 없다.
연구가설(H1): 기존 2019년도 고객 불만율과 2020년도 CS교육 후 불만율에 차이가 있다.
연구환경: 2019년도 114 전화번호 안내고객을 대상으로 불만을 갖는 고객은 20%였다. 이를 개선하기 위해서 2020년도 CS교육을 실시한 후 150명 고객을 대상으로 조사한 결과 14명이 불만이 있었다. 기존 20%보다 불만율이 낮아졌다고 할 수 있는가?
------------------------------------------------------------------------------------------------------------------------------------------------------
1. 단일 표본 대상 기술통계량
분석대상의 단일 표본을 대상으로 빈도분석을 통해서 불만율에 대한 비율을 계산한다
ex) 단일 표본 빈도수와 비율계산
#1 실습 데이터 가져오기
| data <- read.csv("C:/one_sample.csv", header = TRUE) head(data) # no gender survey time # 1 1 2 1 5.1 # 2 2 2 0 5.2 # 3 3 2 1 4.7 # 4 4 2 1 4.8 # 5 5 2 1 5.0 # 6 6 2 1 5.4 |
#2 빈도수와 비율계산
| x <- data$survey x # [1] 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 1 1 1 # [32] 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 # [63] 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 # [94] 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 # [125] 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 summary(X) # Min. 1st Qu. Median Mean 3rd Qu. Max. # 165.1 165.1 165.1 165.1 165.1 165.1 length(x) # 표본수 n # 150 table(x) # x # 0 1 # 14 136 |
#3 패키지를 이용하여 빈도수와 비율 계산
| install.packages("prettyR") library(prettyR) freq(x) # Frequencies for x # 1 0 NA # 136 14 0 # % 90.7 9.3 0 # %!NA 90.7 9.3 |
2. 이항분포 비율 검정
명목척도의 비율을 바탕으로 binom.test()함수를 이용하여 이항분포의 양측 검정을 통해서 검정 통계량을 구한 후 이를 이용하여 가설을 검정한다.
binom.test()함수
정규분포 vs 이항분포 모집단이 가지는 이상적인 분포 형태로 정규분포는 연속변량이지만, 이항분포는 이산변량이며 그래프는 좌우대칭인 종 모양의 곡선 형태를 나타낸다.
binom.test(x, n, p, alternative=c(“two.sided”, “less”, “greater”), conf.level = 0.95)
binom.test(x = 관측도수, n = 표본수, p = 귀무가설_모비율, alternative = "대립가설_종류")
binom.test(x = 관측도수, n = 표본수, p = 귀무가설_모비율,
alternative = "대립가설_종류", conf.level = 신뢰수준) # 신뢰구간의 신뢰수준을 조정
ex) 불만율 기준 비율검정
기존 불만율 20%와 차이가 있는지를 알아보기 위하여 양측 검정을 시행한다.
#1 양측 검정
| binom.test(14, 150, p = 0.2) # Exact binomial test # # data: 14 and 150 # number of successes = 14, number of trials = 150, p-value = # 0.0006735 # alternative hypothesis: true probability of success is not equal to 0.2 # 95 percent confidence interval: # 0.05197017 0.15163853 # sample estimates: # probability of success # 0.09333333 binom.test(14, 150, p = 0.2, alternative = "two.sided", conf.level = 0.95) # Exact binomial test # # data: 14 and 150 # number of successes = 14, number of trials = 150, p-value = # 0.0006735 # alternative hypothesis: true probability of success is not equal to 0.2 # 95 percent confidence interval: # 0.05197017 0.15163853 # sample estimates: # probability of success # 0.09333333 |
양측 검정 결과는 기존 불만율보다 ‘크다’ 또는 ‘작다’는 방향성은 제시되지 않음. 따라서 방향성을 갖는 단측 가설 검정을 통해 기존 집단과 비교하여 신규 집단의 불만율이 개선되었는지를 확인해야 한다.
- 불만율 20% : 모비율 p = 0.2
- 관측도수 : x = 14
- 표본수 : n = 150
#2 방향성을 갖는 단측 가설 검정
| # 1) 2020년 불만율 > 2019년 불만율 binom.test(c(14, 150), p = 0.2, alternative = "greater", conf.level = 0.95) # Exact binomial test # # data: c(14, 150) # number of successes = 14, number of trials = 164, p-value = # 1 # alternative hypothesis: true probability of success is greater than 0.2 # 95 percent confidence interval: # 0.05234697 1.00000000 # sample estimates: # probability of success # 0.08536585 # 2) 2020년 불만율 < 2019년 불만율 binom.test(c(14, 150), p = 0.2, alternative = "less", conf.level = 0.95) # Exact binomial test # # data: c(14, 150) # number of successes = 14, number of trials = 164, p-value = # 4.881e-05 # alternative hypothesis: true probability of success is less than 0.2 # 95 percent confidence interval: # 0.0000000 0.1302327 # sample estimates: # probability of success # 0.08536585 |
(2) 단일 집단 평균 검정(단일 표본 T-검정)
단일 집단의 평균이 어떤 특정한 집단의 평균과 차이가 있는지를 검정
평균차이검정은 정규분포 여부를 판정한 후 결과에 따라 T-검정 또는 윌콕스(Wilcox) 검정을 시행.
정규분포이면 모수 검정인 T-검정
정규분포가 아닌 경우 비모수 검정인 윌콕스(Wilcox)검정으로 평균차이 검정을 시행
ex)--------------------------------------------------------------------------------------------------------------------------------------------------
귀무가설(H0): 국내에서 생산된 노트북과 A사에서 생산된 노트북의 평균 사용시간에 차이가 없다.
연구가설(H1): 국내에서 생산된 노트북과 A사에서 생산된 노트북의 평균 사용시간에 차이가 있다.
연구환경: 국내에서 생산된 노트북 평균 사용시간이 5.2시간으로 파악된 상황에서, A사에서 생산된 노트북 평균 사용시간과 차이가 있는지를 검정하기 위해서 A사의 노트북 150대를 랜덤으로 선정하여 검정을 시행한다.
-----------------------------------------------------------------------------------------------------------------------------------------------------
1. 단일 표본평균 계산
outlier를 제거한 후 변수에 대한 대표값의 성격을 갖는 평균 계산
ex) 단일 표본 평균 계산하기
#1 실습파일 가져오기
| data <- read.csv("C:/one_sample.csv", header = TRUE) str(data) # 'data.frame': 150 obs. of 4 variables: # $ no : int 1 2 3 4 5 6 7 8 9 10 ... # $ gender: int 2 2 2 2 2 2 2 2 2 1 ... # $ survey: int 1 0 1 1 1 1 1 1 0 1 ... # $ time : num 5.1 5.2 4.7 4.8 5 5.4 NA 5 4.4 4.9 ... head(data) # no gender survey time # 1 1 2 1 5.1 # 2 2 2 0 5.2 # 3 3 2 1 4.7 # 4 4 2 1 4.8 # 5 5 2 1 5.0 # 6 6 2 1 5.4 x <- data$time head(X) # 165.1 summary(x) # Min. 1st Qu. Median Mean 3rd Qu. Max. NA's # 3.000 5.000 5.500 5.557 6.200 7.900 41 mean(x) # NA |
#2 데이터 분포 확인/결측치 제거 ( mean 결과 NA )
| mean(x, na.rm=T) # 5.556881 |
x1 <- na.omit(x) mean(x1) # 5.556881 |
- na.omit()함수: na제외 함수
2. 평균 검정 통계량의 특징
평균 검정 통계량은 비율척도와 같은 수치 기반 데이터에 의미가 있다.
특히 분포의 중심위치를 나타내는 대표값의 성격을 가지며, 정규분포에서 도수분포 곡선이 평균값을 중앙으로 하여 좌우대칭인 종모양을 형성한다.
또한 집단 간의 평균에 차이가 있는지를 검정하는 용도로 사용한다.
3. 정규분포 검정
단일 표본평균 차이 검정을 수행하기 전에 데이터의 분포 형태가 정규분포 인지를 먼저 검정해야 한다.
정규분포 검정은 stats패키지에서 제공하는 shapiro.test()함수 사용
검정 결과가 유의수준 0.05보다 큰 경우 정규분포로 본다.
ex) 정규분포 검정
| shapiro.test(x) # Shapiro-Wilk normality test # # data: x # W = 0.99137, p-value = 0.7242 |
shapiro.test(x1) # Shapiro-Wilk normality test # # data: x # W = 0.99137, p-value = 0.7242 |
4. 정규분포 시각화
정규분포 검정 결과를 시각화하여 x1변량의 정규분포 형태 확인
ex) 정규분포 시각화
| par(mfrow = c(1,2)) hist(x) 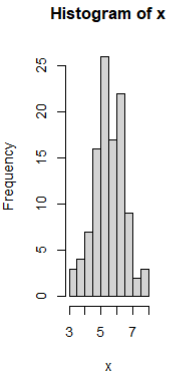 |
- Normal Q-Q Plot
X축: Theoretical Quantile
Y축: Sample Quantile
5. 평균 차이 검정
모집단에서 추출한 표본 데이터의 분포 형태가 정규분포 형태를 가지면, T-검정을 수행 T-검정은 모집단의 평균값을 검정
stats패키지에서 제공하는 t.test()함수 이용
t.test(x, y=NULL, alternative=c(“two.sided”, “less”, “greater”), mu=0, paired=FALSE, var.equal=FALSE, conf.level=0.95,…)
alternavtive속성: 양측검정 또는 단측 검정 수행 가능
conf.level속성: 신뢰수준 지정
mu속성: 비교할 기존 모집단의 평균값 지정
ex) 단일 표본평균 차이 검정
#1 양측 검정 – x1객체의 기존 모집단의 평균 5.2시간 비교
| t.test(x,mu=5.2) # One Sample t-test # # data: x # t = 3.9461, df = 108, p-value = 0.0001417 # alternative hypothesis: true mean is not equal to 5.2 # 95 percent confidence interval: # 5.377613 5.736148 # sample estimates: # mean of x # 5.556881 qqnorm(x)  qqline(x, lty = 1, col = "blue")  t.test(x, mu=5.2, alter = "two.side", conf.level = 0.95) # One Sample t-test # # data: x # t = 3.9461, df = 108, p-value = 0.0001417 # alternative hypothesis: true mean is not equal to 5.2 # 95 percent confidence interval: # 5.377613 5.736148 # sample estimates: # mean of x # 5.556881 |
p-value < α 때문에 국내에서 생산된 노트북과 A사에서 생산된 노트북의 평균 사용 시간에 차이가 있다고 볼 수 있다.
#2 방향성을 갖는 단측 가설 검정
| t.test(x, mu = 5.2, alter= "greater", conf.level = 0.95) # One Sample t-test # # data: x # t = 3.9461, df = 108, p-value = 7.083e-05 # alternative hypothesis: true mean is greater than 5.2 # 95 percent confidence interval: # 5.406833 Inf # sample estimates: # mean of x # 5.556881 |
#3 귀무가설의 임계값 계산
| qt(0.05, 108, lower.tail=F) # 1.659085 |
stats패키지에서 제공하는 qt()함수: 귀무가설의 임계값(귀무가설을 기각할 수 있는 임계값 계산)
qt(p-value, df, lower.tail=T)
- lower.tail=T (default): P(X <=x)
- lower.tail=F : P(X > x)
통계 분포 함수 내 접두어
d(ensity): 확률 밀도 함수 값 구하기
P{X=x} p(robability): 누적분포 함수에 의한 누적확률 구하기 P(X < x)
q(uantile): 누적확률에 해당하는 분위 구하기
r(andom): 난수생성
6. 단일 집단 T-검정 결과 작성
논문이나 보고서에서 단일 표본평균 검정 결과를 제시