59doit
[ R ] 회귀분석 #2 다중회귀분석 본문
(3) 다중 회귀분석
여러 개의 독립변수가 동시에 한 개의 종속변수에 미치는 영향을 분석할 때 이용하는 분석 방법
공차한계(Tolerance) : 한 독립변수가 다른 독립변수들에 의해서 설명되지 않은 부분
분산팽창요인(Variance Inflation Factor, VIF) : 공차한계의 역수
다중 공선성(Multicollinearity)문제
다중 공선성: 한 독립변수의 값이 증가할 때 다른 독립변수의 값이 증가하거나 감소하는 현상
독립변수들이 강한 상관관계를 보이는 경우는 회귀분석의 결과를 신뢰하기 어렵다.
상관관계가 높은 독립 변수 중 하나 혹은 일부를 제거하거나 변수를 변형시켜서 해결
독립변수 제거를 통한 정보손실 vs. 다중 공선성 문제 해결 → 판단 필요
귀무가설: 적절성과 친밀도는 제품의 만족도에 영향을 미친다고 볼 수 없다.
대립가설: 적절성과 친밀도는 제품의 만족도에 영향을 미친다고 볼 수 있다
ex) 다중 회귀분석
#1 변수 모델링
| y=product$제품_만족도 x1=product$제품_친밀도 x2=product$제품_적절성 df <- data.frame(x1,x2,y) |
#2 다중 회귀분석
| result.lm <- lm(formula=y~x1+x2,data=df) result.lm # Call: # lm(formula = y ~ x1 + x2, data = df) # # Coefficients: # (Intercept) x1 x2 # 0.66731 0.09593 0.68522 |
ex) 다중 공선성(Multicollinearity)문제 확인
#1 패키지 설치
| install.packages("car") library(car) |
#2 분산팽창요인(VIF)
| vif(result.lm) # x1 x2 # 1.331929 1.331929 |
ex) 다중 회귀분석 결과보기
| summary(result.lm) # Call: # lm(formula = y ~ x1 + x2, data = df) # # Residuals: # Min 1Q Median 3Q Max # -2.01076 -0.22961 -0.01076 0.20809 1.20809 # # Coefficients: # Estimate Std. Error t value Pr(>|t|) # (Intercept) 0.66731 0.13094 5.096 6.65e-07 *** # x1 0.09593 0.03871 2.478 0.0138 * # x2 0.68522 0.04369 15.684 < 2e-16 *** # --- # Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # # Residual standard error: 0.5278 on 261 degrees of freedom # Multiple R-squared: 0.5975, Adjusted R-squared: 0.5945 # F-statistic: 193.8 on 2 and 261 DF, p-value: < 2.2e-16 |
결과 제시 방법 가설, 분석결과, 가설검정, 회귀모형 결정계수, 수정결정계수, 회귀모형의 적합성, 독립변수 설명
(4) 다중 공선성 문제 해결과 모델 성능평가
다중 공선성 문제 해결 방법 실습순서: 다중 공선성 문제 해결 회귀모델 생성 예측치 생성 모델 성능평가
(1) 다중 공선성 문제 해결
다중 공선성 문제: 독립변수 간의 강한 상관관계로 인하여 회귀분석의 결과를 신뢰할 수 없는 현상 강한 상관관계를 갖는 독립변수를 제거하여 해결
ex) 다중 공선성 문제 확인
#1 패키지 설치 및 데이터 로딩
| install.packages("car") library(car) data(iris) |
#2 iris 데이터 셋으로 다중 회귀분석
| model <- lm(formula = Sepal.Length ~ Sepal.Width + Petal.Length + Petal.Width, data = iris) vif(model) # Sepal.Width Petal.Length Petal.Width # 1.270815 15.097572 14.234335 sqrt(vif(model)) > 3 # Sepal.Width Petal.Length Petal.Width # FALSE TRUE TRUE |
#3 iris 변수 간의 상관계수 구하기
| cor(iris[,-5]) # Sepal.Length Sepal.Width Petal.Length Petal.Width # Sepal.Length 1.0000000 -0.1175698 0.8717538 0.8179411 # Sepal.Width -0.1175698 1.0000000 -0.4284401 -0.3661259 # Petal.Length 0.8717538 -0.4284401 1.0000000 0.9628654 # Petal.Width 0.8179411 -0.3661259 0.9628654 1.0000000 |
상관계수로 변수간의 강한 상관관계 구분
(2) 회귀모델 생성
동일한 데이터 셋을 7:3 비율로 학습데이터와 검정데이터로 표본 추출한 후 학습데이터를 이용하여 회귀모델을 생성
ex) 데이터 셋 생성과 회귀모델 생성
#1 학습데이터와 검정데이터 표본 추출
| x <- sample(1:nrow(iris),0.7*nrow(iris)) train <- iris[x,] test <- iris[-x,] |
sample()함수 이용하여 70% 데이터 추출하여 학습데이터, 나머지 데이터는 검정데이터로 설정
다중 공선성 문제가 발생하는 Petal.Width변수를 제거한 후 학습데이터를 이용하여 회귀모델 생성
#2 변수 제거 및 다중 회귀분석
| model <- lm(formula = Sepal.Length ~ Sepal.Width + Petal.Length, data = train) model # Call: # lm(formula = Sepal.Length ~ Sepal.Width + Petal.Length, data = train) # # Coefficients: # (Intercept) Sepal.Width Petal.Length # 2.2251 0.6200 0.4614 summary(model) # Call: # lm(formula = Sepal.Length ~ Sepal.Width + Petal.Length, data = train) # # Residuals: # Min 1Q Median 3Q Max # -0.95132 -0.23691 -0.02525 0.21571 0.80048 # # Coefficients: # Estimate Std. Error t value Pr(>|t|) # (Intercept) 2.22509 0.29653 7.504 2.39e-11 *** # Sepal.Width 0.62003 0.08542 7.259 7.93e-11 *** # Petal.Length 0.46137 0.02021 22.833 < 2e-16 *** # --- # Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # # Residual standard error: 0.34 on 102 degrees of freedom # Multiple R-squared: 0.8368, Adjusted R-squared: 0.8336 # F-statistic: 261.4 on 2 and 102 DF, p-value: < 2.2e-16 |
(3) 회귀방정식 도출
절편, 기울기, 독립변수(x)의 관측치를 이용하여 회귀방정식을 도출
ex) 회귀방정식 도출
#1 회귀방정식을 위한 절편과 기울기 보기
| model # Call: # lm(formula = Sepal.Length ~ Sepal.Width + Petal.Length, data = train) # # Coefficients: # (Intercept) Sepal.Width Petal.Length # 2.2251 0.6200 0.4614 |
#2 회귀방정식 도출
| head(train,1) # Sepal.Length Sepal.Width Petal.Length Petal.Width Species # 32 5.4 3.4 1.5 0.4 setosa |
(4) 회귀방정식 도출
검정데이터를 이용하여 회귀모델의 예측치를 생성.
학습데이터에 의해 생성된 회귀모델을 검정데이터에 적용하여 모델의 예측치를 생성 predict()함수
predict(model, data)
model: 회귀모델(회귀분석 결과가 저장된 객체)
data: 독립변수(x)가 존재하는 검정데이터 셋
ex) 검정데이터의 독립변수를 이용한 예측치 생성
| pred <- predict(model,test) pred |
(5) 회귀모델 평가
모델평가는 일반적으로 상관계수를 이용 모델의 예측치(pred)와 검정데이터의 종속변수(y)를 이용하여 상관계수(r)를 구하여 모델의 분류정확도를 평가한다. 상관관계가 높다면 분류정확도가 높다고 볼 수 있음.
ex) 상관계수를 이용한 회귀모델 평가
| cor(pred,test$Sepal.Length) # 0.9239866 |
(5) 기본 가정 충족으로 회귀분석 수행
회귀분석은 선형성, 다중 공선성, 잔차의 정규성 등 몇가지 기본 가정이 충족되어야 수행할 수 있는 모수 검정방법 회귀분석의 기본 가정을 충족하는지 확인
ex) 회귀분석의 기본 가정 충족으로 회귀분석 수행
#1회귀모델 생성
#1-1 변수 모델링
| formula = Sepal.Length ~ Sepal.Width + Petal.Length + Petal.Width |
#1-2 회귀모델 생성
| model <- lm(formula=formula, data=iris) model # Call: # lm(formula = formula, data = iris) # # Coefficients: # (Intercept) Sepal.Width Petal.Length Petal.Width # 1.8560 0.6508 0.7091 -0.5565 |
#2 잔차(오차)분석
#2-1 독립성 검정 – 더빈 왓슨 값으로 확인
| install.packages('lmtest') library(lmtest) dwtest(model) # Durbin-Watson test # # data: model # DW = 2.0604, p-value = 0.6013 # alternative hypothesis: true autocorrelation is greater than 0 |
더빈 왓슨 값의 p-value가 0.05이상(DW값 1-3범위)이면 잔차에 유의미한 자기 상관이 없다고 볼 수 있다. 즉 독립성이 있다고 볼 수 있다.
#2-2 등분산성 검정 – 잔차와 적합값의 분포
plot(model,which=1)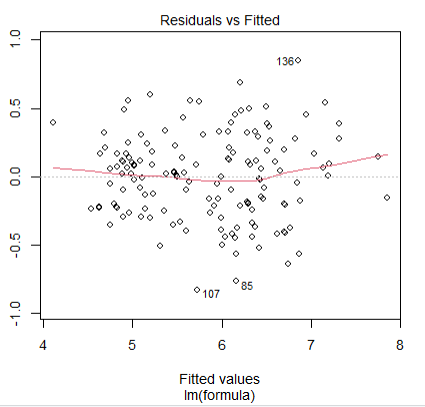 |
잔차(residual) 0을 기준으로 적합값(fitted values)의 분포가 좌우 균등하면 잔차들은 등분산성과 차이가 없다고 볼 수 있다.
#2-3 잔차의 정규성 검정
| attributes(model) # $names # [1] "coefficients" "residuals" "effects" "rank" # [5] "fitted.values" "assign" "qr" "df.residual" # [9] "xlevels" "call" "terms" "model" # # $class # [1] "lm" res <- residuals(model) shapiro.test(res) # Shapiro-Wilk normality test # # data: res # W = 0.99559, p-value = 0.9349 |
shapiro.test()함수 이용하여 정규성 검정 hist()함수로 히스토그램과 qqnorm()함수를 통해 Normal Q-Q plot으로 정규성 확인 가능
#3 다중 공선성 검사
| library(car) sqrt(vif(model))>3 # Sepal.Width Petal.Length Petal.Width # FALSE TRUE TRUE |
Petal.Length와 Petal.Width변수 간에는 다중 공선성 문제가 의심스러워 두 변수 중 하나 제거하여 회귀모델 다시 생성
#4 회귀모델 생성과 평가
| formula = Sepal.Length ~ Sepal.Width + Petal.Length model <- lm(formula = formula, data = iris) summary(model) # Call: # lm(formula = formula, data = iris) # # Residuals: # Min 1Q Median 3Q Max # -0.96159 -0.23489 0.00077 0.21453 0.78557 # # Coefficients: # Estimate Std. Error t value Pr(>|t|) # (Intercept) 2.24914 0.24797 9.07 7.04e-16 *** # Sepal.Width 0.59552 0.06933 8.59 1.16e-14 *** # Petal.Length 0.47192 0.01712 27.57 < 2e-16 *** # --- # Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # # Residual standard error: 0.3333 on 147 degrees of freedom # Multiple R-squared: 0.8402, Adjusted R-squared: 0.838 # F-statistic: 386.4 on 2 and 147 DF, p-value: < 2.2e-16 |
Petal.Width제거 후 회귀모델 생성 모델이 유의하고 모델의 설명력(Adjusted R square)가 높음
'통계기반 데이터분석' 카테고리의 다른 글
| [ R ] 시계열분석 #1 (1) | 2022.11.28 |
|---|---|
| [ R ] 로지스틱 회귀분석 (0) | 2022.11.28 |
| [ R ] 회귀분석 #1 단순회귀분석 (0) | 2022.11.27 |
| [ R ] 요인분석 #3 잘못 분류된 요인 제거로 변수 정제 (0) | 2022.11.26 |
| [ R ] 요인분석 #2 요인점수를 이용한 요인적재량 시각화 (0) | 2022.11.26 |



