59doit
[ R ] 시계열분석 #1 본문
시계열분석
어떤 현상에 대해서 시간의 변화량을 기록한 시계열 자료를 대상으로 미래의 변화에 대한 추세를 분석하는 방법
시계열 자료: 시간의 변화에 따라 관측치 또는 통계량의 변화를 기록해 놓은 자료
시계열 분석은 현재의 현상 이해를 기초로 미래를 예측하는 분석 방법 경기예측, 판매예측, 주식시장분석, 예산 및 투자 분석 등의 분야에서 활용
(1) 시계열 분석의 특징
시계열분석은 설명변수와 반응변수를 토대로 유의수준에 의해서 판단하는 추론 통계방식
< 시계열분석의 특징과 분석에 사용되는 데이터 셋의 전제조건 >
- y변수 존재: 시간 t를 설명변수(x)로 시계열을 반응변수(y)로 사용
- 미래추정: 과거와 현재의 현상을 파악하고 이를 통해 미래를 추정
- 계절성 자료: 시간 축을 기준으로 계절성이 있는 자료를 데이터 셋으로 이용
- 모수 검정: 선형성, 정규성, 등분산성 가정을 만족해야 한다.
- 추론 기능: 유의수준 판단 기준이 존재하는 추론통계 방식
- 활용분야: 경기예측, 판매예측, 주식시장분석, 예산 및 투자 분석 등에서 활용
(2) 시계열분석의 적용 범위
< 회귀분석 vs. 시계열 분석 >
- 회귀분석: 데이터의분포나 두 데이터 간의 상관성을 토대로 분석
- 시계열분석: 어떤 시간의 변화에 따라 현재 시점(t)의 자료와 이전시점(t-1)의 자료 간의 상관성을 토대로 분석
< 시계열분석의 적용 사례 >
- 기존 사실에 관한 결과 규명: 고객의 구매패턴 분석
- 시계열 자료 특성 규명: 시계열에 영향을 주는 추세, 계절, 순환, 불규칙 요소를 분해해서 분석(시계열 요소 분해법)
- 가까운 미래에 대한 시나리오 규명
- 변수와 변수의 관계 규명: 경기선행지수와 종합주가지수의 관계 분석의 사례
- 변수 제어 결과 규명: 입력변수의 제어(조작)를 통해서 미래의 예측결과를 통제
시계열 자료분석
시계열 자료는 크게 정상성 시계열과 비정상성 시계열로 구분
대부분의 시계열 자료는 비정상성 시계열 자료
(1) 시계열 자료 구분
정상성(stationary)시계열: 시계열 자료의 변화 패턴이 일정한 평균값을 중심으로 일정한 변동 폭을 갖는 시계열
비정상(non-stationary)시계열: 정상성 시계열이 아닌 시계열 자료
(2) 시계열 자료 확인
정상성 시계열은 평균이 0이며 일정한 분산을 갖는 정규분포에서 추출된 임의의 값으로 불규칙성(독립적)을 갖는 데이터로 정의
백색 잡음(whitenoise): 이러한 불규칙성을 갖는 패턴
비정상성 시계열은 규칙성(비독립성)을 갖는 패턴으로 시간의 추이에 따라서 점진적으로 증가하거나 하강하는 추세(Trend)의 규칙, 일정한 주기(cycle)단위로 동일한 규칙이 반복되는 계절성(Seasonality)의 규칙을 보인다.
이러한 비정상성 시계열은 시계열 자료의 추세선, 시계열 요소분해, 자기상관 함수의 시각화 등을 통해서 확인할 수 있다.
시계열 자료가 비정상성 시계열이면 정상성 시계열로 변화시켜야 시계열 모형을 생성할 수 있다.
< 정상성 시계열로 변환시키키는 대표적 방법 >
- 차분(Differencing): 현재 시점에서 이전 시점의 자료를 빼는 연산으로 평균을 정상화하는데 이용
- 로그변환: log()함수를 이용하여 분산을 정상화하는데 이용
ex) 비정상성 시계열을 정상성 시계열로 변경
#1 AirPassengers 데이터 셋 가져오기
| data(AirPassengers) |
#2 차분 적용 – 평균 정상화
| par(mfrow=c(1,2)) ts.plot(AirPassengers) diff <- diff(AirPassengers) plot(diff)  |
ts.plot()함수: 시계열 시각화
diff()함수: 차분
차분을 수행한 결과가 대체로 일정한 값을 얻으면 선형의 추세를 갖는다는 판단 가능
만약, 시계열에 계절성이 있으면 계절 차분을 수행하여 정상성 시계열로 변경
차분된 것을 다시 차분했을 때 일정한 값들을 보인다면 그 시계열 자료는 2차식의 추세를 갖는다고 판단
#3 로그 적용 – 분산 정상화
| par(mfrow=c(1,2)) plot(AirPassengers) log <- diff(log(AirPassengers)) plot(log) 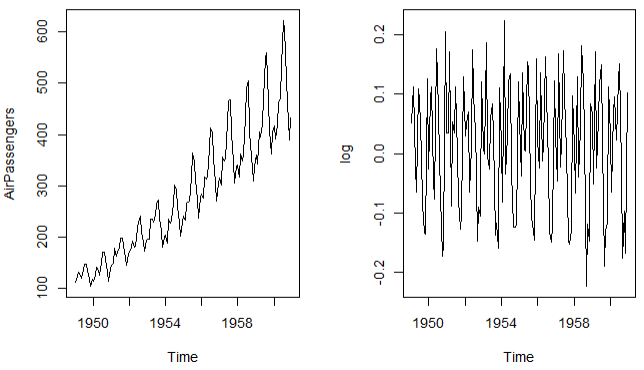 |
시계열 자료 시각화
(1) 시계열 추세선 시각화
추세선: 어떤 현상이 일정한 방향으로 나아가는 경향이 직선이나 곡선 형태로 차트에서 나타내는 선
ex) 단일 시계열 자료 시각화
#1 데이터불러오기
| data("WWWusage") str(WWWusage) WWWusage |
#2 시계열 자료 추세선 시각화
| X11() ts.plot(WWWusage,type="l",col="red")  |
X11()함수: 새로운 창에서 시각화
ex) 다중 시계열 자료 시각화
EuStockMarkets 데이터 셋 사용
#1 데이터불러오기
| data(EuStockMarkets) head(EuStockMarkets) # DAX SMI CAC FTSE # [1,] 1628.75 1678.1 1772.8 2443.6 # [2,] 1613.63 1688.5 1750.5 2460.2 # [3,] 1606.51 1678.6 1718.0 2448.2 # [4,] 1621.04 1684.1 1708.1 2470.4 # [5,] 1618.16 1686.6 1723.1 2484.7 # [6,] 1610.61 1671.6 1714.3 2466.8 |
#2 데이터프레임으로 변환
| EuStock <- data.frame(EuStockMarkets) head(EuStock) # DAX SMI CAC FTSE # 1 1628.75 1678.1 1772.8 2443.6 # 2 1613.63 1688.5 1750.5 2460.2 # 3 1606.51 1678.6 1718.0 2448.2 # 4 1621.04 1684.1 1708.1 2470.4 # 5 1618.16 1686.6 1723.1 2484.7 # 6 1610.61 1671.6 1714.3 2466.8 |
#3 단일 시계열 자료 추세선 시각화(1,000개 데이터 대상
| X11() plot(EuStock$DAX[1:1000],type="l",col='red')  |
#4 다중 시계열 자료 추세선 시각화(1,000개 데이터 대상)
| plot.ts(cbind(EuStock$DAX[1:1000],EuStock$SMI[1:1000]), main=("주가지수 추세선"))  |
plot.ts()함수: 시계열 자료 plot
(2) 시계열 요소 분해 시각화
< 시계열 자료의 변동요인 >
- 추세변동(Trend variation: T): 상승과 하락의 영향을 받아 시계열 자료에 영향을 주는 장기 변동요인
- 순환변동(Cyclical variation: C): 일정한 기간 없이 반복적인 요소를 가지는 중/장기 변동요인
- 계정변동(seasonal variation: S): 일정기간에 의해서 1년 단위로 반복적인 요소를 가지는 단기 변동요인
- 불규칙변동(Irregular variation: I): 어떤 규칙 없이 예측 불가능한 변동요인으로 추세, 순환, 계절요인으로 설명할 수 없는 요인. 실제 시계열 자료에서 추세, 순환, 계절요인을 뺀 결과로 나타난다. 이는 회귀분석에서 오차에 해당
ex) 시계열 요소 분해 시각화
#1 시계열 자료 준비
| data <- c(45, 56, 45, 43, 69, 75, 58, 59, 66, 64, 62, 65, 55, 49, 67, 55, 71, 78, 71, 65, 69, 43, 70, 75, 56, 56, 65, 55, 82, 85, 75, 77, 77, 69, 79, 89) length(data) |
#2 시계열 자료 생성 – 시계열 자료 형식으로 객체 생성
| tsdata <- ts(data,start=c(2016,1),frequency = 12) tsdata # Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec # 2016 45 56 45 43 69 75 58 59 66 64 62 65 # 2017 55 49 67 55 71 78 71 65 69 43 70 75 # 2018 56 56 65 55 82 85 75 77 77 69 79 89 |
frequency = 12 : 12개월
#3 추세선 확인 – 각 요인(추세, 순환, 계절, 불규칙)을 시각적으로 확인
ts.plot(tsdata) |
#4 시계열 분해
plot(stl(tsdata,"periodic")) |
stl()함수: 하나의 시계열 자료를 대상으로 시계열 변동요인인 계절요소(seasonal), 추세(trend), 잔차(remainder)를 제공
#5 시계열 분해와 변동요인 제거
| m <- decompose(tsdata) attributes(m) plot(m)  par(mfrow=c(1,1)) plot(tsdata-m$seasonal)  |
#6 추세요인과 불규칙요인 제거
plot(tsdata-m$trend) plot(tsdata-m$seasonal-m$trend)  |
(3) 자기 상관 함수/부분 자기 상관 함수 시각화
자기 상관성: 자기 상관계수가 유의미한가를 나타내는 특성
자기 상관계수(Auto Correlation Function, ACF): 시계열 자료(Yt)에서 시차(lag)를 일정하게 주는 경우 얻어지는 상관계수 예) 시차1의 자기 상관계수는 Yt와 Yt-1 간의 상관계수
부분 자기 상관계수(Partial Auto Correlation Function, PACF): 다른 시차들의 시계열 자료가 미치는 영향을 제거한 후에 주어진 시차에 대한 시계열 간의 상관계수
자기 상관 함수와 부분 자기 상관 함수는 시계열의 모형을 식별하는 수단으로 이용
ex) 시계열 요소 분해 시각화
#1 시계열 자료 생성
| input <- c(3180, 3000, 3200, 3100, 3300, 3200, 3400, 3550, 3200, 3400, 3300, 3700) length(input) tsdata <- ts(input, start = c(2015, 2), frequency = 12) |
#2 자기 상관 함수 시각화
acf(na.omit(tsdata), main="자기상관함수",col="red") |
점선은 유의미한 자기 상관관계에 대한 임계값을 의미
모든 시차(lag)가 파란 점선 안쪽에 있기 때문에 서로 이웃한 시점 간의 자기 상관성은 없는 것으로 해석
#3 부분 자기 상관 함수 시각화
pacf(na.omit(tsdata), main="부분분자기상관함수",col="red") |
자기 상관 함수에 의해서 주기 생성에는 어떤 종류의 시간 간격이 영향을 미치는가를 보여주고 있다.
모든 시차가 점선 안에 있기 때문에 주어진 시점 간의 자기 상관성은 없는 것으로 해석
(4) 추세 패턴 찾기 시각화
추세패턴: 시계열 자료가 증가 또는 감소하는 경향이 있는지 알아보고, 증가 또는 감소하는 경향이 선형(linear)인지 비선형(nonlinear)인지를 찾는 과정
추세 패턴의 객관적인 근거는 차분(Differencing)과 자기 상관성(Autocorrelation)을 통해서 얻을 수 있다
ex) 시계열 자료의 추세 패턴 찾기 시각화
#1 시계열 자료 생성
| input <- c(3180, 3000, 3200, 3100, 3300, 3200, 3400, 3550, 3200, 3400, 3300, 3700) |
#2 추세선 시각화
plot(tsdata,type="l",col="red") |
#3 자기 상관 함수 시각화
acf(na.omit(tsdata), main="자기상관함수",col="red") |
#4 차분 시각화
plot(diff(tsdata,differences=1)) |
'통계기반 데이터분석' 카테고리의 다른 글
| [ R ] 의사결정나무 #1 (0) | 2022.11.29 |
|---|---|
| [ R ] 시계열분석 #2 (0) | 2022.11.28 |
| [ R ] 로지스틱 회귀분석 (0) | 2022.11.28 |
| [ R ] 회귀분석 #2 다중회귀분석 (0) | 2022.11.27 |
| [ R ] 회귀분석 #1 단순회귀분석 (0) | 2022.11.27 |




