59doit
[ R ] 군집분석 #2 본문
군집분석
데이터 간의 유사도를 정의하고, 그 유사도에 가까운 것부터 순서대로 합쳐 가는 방법으로 그룹(군집)을 형성한 후 각 그룹의 성격을 파악하거나 그룹 간의 비교분석을 통해서 데이터 전체의 구조에 대한 이해를 돕고자 하는 탐색적인 분석 방법
*유사도: 거리(distance)를 이용하는데 거리의 종류는 다양하지만, 가장 일반적으로 사용하는 것이 유클리디안(Euclidean)거리로 측정한 거리정보를 이용해서 분석대상을 몇 개의 집단으로 분류
- 군집 분석의 목적:
데이터 셋 전체를 대상으로 서로 유사항 개체 들을 몇 개의 군집으로 세분화하여 대상 집단을 정확하게 이해하고, 효율적으로 활용하기 위함. 군집 분석으로 그룹화된 군집은 변수의 특성이 그룹 내적으로는 동일하고, 외적으로는 이질적인 특성을 갖는다.
- 군집 분석의 용도
고객의 충성도에 따라서 몇 개의 그룹으로 분류하고, 그룹별로 맞춤형 마케팅 및 프로모션 전략을 수립하는 데 활용된다.
- 군집 분석에서 중요한 사항:
군집화를 위해서 거리 측정에 사용되는 변인은 비율척도나 등간척도여야 하며, 인구 통계적 변인, 구매패턴 변인, 생활패턴 변인 등이 이용된다.
군집 분석에 사용되는 입력 자료는 변수의 측정단위와 관계없이 그 차이에 따라 일정하게 거리를 측정하기 때문에 변수를 표준화하여 사용하는 것이 필요하다.
군집화 방법에 따라 계층적 군집 분석과 비계층적 군집분석으로 분류된다.
- 군집 분석에 이용되는 변인
인구 통계적 변인: 거주지, 성별, 나이, 교육수준, 직업, 소득수준 등
구매패턴 변인: 구매상품, 1회 평균 거래액, 구매획수, 구매주기 등
생활패턴 변인: 생활습관, 가치관, 성격, 취미 등
- 군집 분석의 특징
전체적인 데이터 구조를 파악하는데 이용된다.
관측대상 간 유사성을 기초로 비슷한 것끼리 그룹화(clustering)한다.
유사성은 유클리디안 거리를 이용한다. 분석 결과에 대한 가설검정이 없다.
반응변수(y변수)가 존재하지 않는 데이터마이닝 기법이다.
규칙(Rule)을 기반으로 계층적인 트리구조를 생성한다.
활용분야: 구매패턴에 따른 고객 분류, 충성도에 따른 고객 분류 등
- 군집 분석의 절차
1) 분석대상의 데이터에서 군집 분석에 사용할 변수 추출
2) 계층적 군집 분석을 이용한 대략적인 군집의 수 결정
3) 계층적 군집 분석에 대한 타당성 검증(ANOVA분석)
4) 비계층적 군집 분석을 이용한 군집 분류
5) 분류된 군집의 특성 파악 및 업무 적용
- 군집의 종류
1. 계층적 군집(Hierarchical Clustering): 트리 구조처럼 분리하는 방법
1) 병합(agglomeration)방법
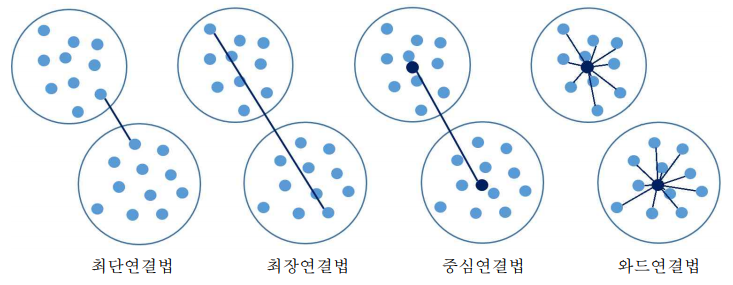
- 단일(최단)연결법(Single Linkage Method) : 또는 단일연결법(single linkage method)은 두 군집 사이의 거리를 각 군집 에서 하나씩 관측 값을 뽑았을 때 나타날 수 있는 거리의 최솟값으로 측정한다. 최단거리를 사용할 때 사슬 모양으로 생길 수 있으며, 고립된 군집을 찾는데 중점을 둔 방법
- 완전(최장)연결법(Complete Linkage Method) : 또는 완전연결법(complete linkage method)은 두 군집 사이의 거리를 각 군 집에서 하나씩 관측 값을 뽑았을 때 나타날 수 있는 거리의 최댓값으로 측정한다. 같은 군 집에 속하는 관측치는 알려진 최대 거리보다 짧으며, 군집들의 내부 응집성에 중점을 둔 방법
- 평균연결법(Average Linkage Method) : 모든 항목에 대한 거리 평균을 구하면서 군집화를 하기 때문에 계산양이 불필요하게 많아질 수 있다.
- 중심연결법(Centroid Linkage Method) : 두 군집의 중심 간의 거리를 측정한다. 두 군집이 결합될 때 새로운 군집의 평균은 가중평균을 통해 구해진다.
- Ward 연결법(Ward Linkage Method) : 군집간의 거리에 기반하는 다른 연결법과는 달 리 군집내의 오차제곱합(error sum of square)에 기초하여 군집을 수행한다. 보통 두 군집 이 합해지면 병합된 군집의 오차제곱합은 병합 이전 각 군집의 오차제곱합의 합 보다 커지 게 되는데, 그 증가량이 가장 작아지는 방향으로 군집을 형성해 나가는 방법이다. 와드연결 법은 크기가 비슷한 군집끼리 병합
2) 분할(Division)방법
- 다이아나 방법(DIANA Method)
2. 분할적 군집: 특정 점을 기준으로 가까운 것끼리 묶는 방법
1) 프로토타입(Prototype Based) :
- K-중심군집(K-Medoids Clustering)
- 퍼지군집(Fuzzy Clustering)
2) 밀도기반(Density Based) :
- 중심 밀도 군집(Center Density Clustering)
- 격자 기반 군집(Grid Based Clustering)
- 커널 기반 군집(Kernel Based Clustering)
3) 분포기반(Distribution Based)
- 혼합분포 군집(Mixture Distribution Clustering)
4) 그래프 기반(Graph Based)
- 코호넨 군집(Kohonen Clustering)
(1) 유클리디안 거리
유클리디안 거리 계산식
ex) 유클리디안 거리 계산법
#1 matrix 객체 생성
| x <- matrix(1:9, nrow = 3, by = T) x # [,1] [,2] [,3] # [1,] 1 2 3 # [2,] 4 5 6 # [3,] 7 8 9 |
#2 유클리디안 거리 생성
| dist <- dist(x, method = "euclidean") dist # 1 2 # 2 5.196152 # 3 10.392305 5.196152 |
dist()함수 형식: dist(x, method = “euclidean”)
ex) 1행과 2행 변량의 유클리디안 거리 구하기
| # x # [,1] [,2] [,3] # [1,] 1 2 3 # [2,] 4 5 6 # [3,] 7 8 9 s <- sum((x[1, ] - x[2, ]) ^ 2) s # 27 sqrt(s) # 5.196152 |
s 는 (1-4)^ 2 , (2-5)^ 2 , (3-6)^ 2 을 모두 더한 값
ex) 1행과 3행 변량의 유클리디안 거리 구하기
| s <- sum((x[1,] - x[3,]) ^ 2) s # 108 sqrt(s) # 10.3923 |
s 는 (1-7)^ 2 , (2-8)^ 2 , (3-9)^ 2 을 모두 더한 값
(2) 계층적 군집 분석
계층적 군집 분석(Hierarchical Clustering): 개별대상 간의 거리에 의하여 가장 가까운 대상부터 결합하여 나무 모양의 계층구조를 상향식(Bottom-up)으로 만들어가면서 군집을 형성
군집 대상 간의 거리를 산정하는 기준에 따라
단일(최단)연결법(Single Linkage Method): 최소거리 기준
완전(최장)연결법(Complete Linkage Method): 최대거리 기준
평균연결법(Average Linkage Method): 평균 거리 기준
중심연결법(Centroid Linkage Method): 중심값의 거리 기준
Ward 연결법(Ward Linkage Method): 유클리디안 제공 거리 기준
장점: 군집이 형성되는 과정을 파악
단점: 자료의 크기가 큰 경우 분석이 어렵다
ex) 유클리디안 거리를 이용한 군집화
#1 군집 분석(Clustering)을 위한 패키지 설치
| install.packages("cluster") library(cluster) |
#2 데이터 셋 생성
| x <- matrix(1:9, nrow = 3, by = T) x # [,1] [,2] [,3] # [1,] 1 2 3 # [2,] 4 5 6 # [3,] 7 8 9 |
#3 matrix 객체 대상 유클리디안 거리 생성
| dist <- dist(x, method = "euclidean") dist # 1 2 # 2 5.196152 # 3 10.392305 5.196152 |
dist함수 사용
#4 유클리디안 거리 matrix를 이용한 군집화
| hc <- hclust(dist) hc # Call: # hclust(d = dist) # # Cluster method : complete # Distance : euclidean # Number of objects: 3 |
hclust()함수를 사용하여 모델생성
#5 클러스터 시각화
plot(hc)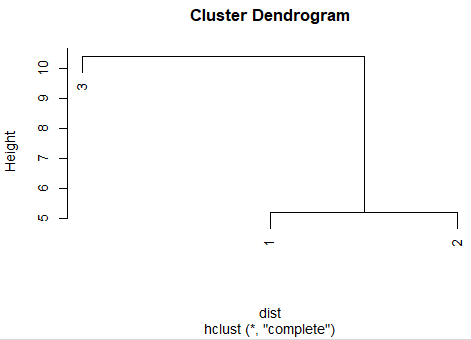 |
ex) 신입사원의 면접시험 결과를 군집 분석
#1 데이터 셋 가져오기
| interview <- read.csv("C:/interview.csv", header = TRUE) names(interview) # [1] "no" "가치관" "전문지식" "발표력" "인성" # [6] "창의력" "자격증" "종합점수" "합격여부" head(interview) # no 가치관 전문지식 발표력 인성 창의력 자격증 종합점수 합격여부 # 1 101 20 15 15 15 12 1 77 합격 # 2 102 19 15 14 18 13 1 79 합격 # 3 103 12 16 20 11 7 1 66 불합격 # 4 104 18 15 15 14 13 1 75 합격 # 5 105 9 18 20 9 5 0 61 불합격 # 6 106 20 13 18 15 11 1 77 합격 |
#2 유클리디안 거리 계산
| interview_df <- interview[c(2:7)] # 문자포함된 열 제외하고 유클리디안 거리 계산하기 interview_df idist <- dist(interview_df) idist head(idist) # [1] 3.464102 11.445523 2.449490 15.524175 3.741657 14.142136 |
#3 계층적 군집 분석
| hc <- hclust(idist) hc # Call: # hclust(d = idist) # # Cluster method : complete # Distance : euclidean # Number of objects: 15 |
#4 군집 분석 시각화
plot(hc,hang=-1) 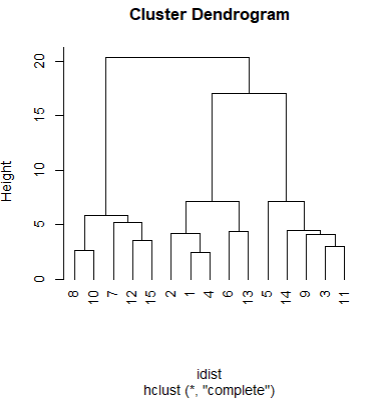 |
plot(hc,hang=2) |
plot()함수의 “hang = -1” 속성을 이용하여 덴드로그램에서 음수값 제거
hang 의 지정 숫자에 따라 달라지는 덴드로그램 모양을 확인 할 수 있다.
#5 군집 테두리 생성
rect.hclust(hc, k = 3, border ="red")  |
k=3 : 군집수 3개
border="red" : 빨간선
ex) 군집별 특징 보기
#1 군집별 서브 셋 만들기
| g1 <- subset(interview, no == 108 | no == 110 | no == 107 | no == 112 | no == 115) g2 <- subset(interview, no == 102 | no == 101 | no == 104 | no == 106 | no == 113) g3 <- subset(interview, no == 105 | no == 114 | no == 109 | no == 103 | no == 111) |
#2 각 서브 셋의 요약통계량 보기
| summary(g1) # no 가치관 전문지식 발표력 # Min. :107.0 Min. :13.0 Min. :17.0 Min. : 8.0 # 1st Qu.:108.0 1st Qu.:14.0 1st Qu.:18.0 1st Qu.:10.0 # Median :110.0 Median :14.0 Median :19.0 Median :11.0 # Mean :110.4 Mean :14.4 Mean :18.8 Mean :10.8 # 3rd Qu.:112.0 3rd Qu.:15.0 3rd Qu.:20.0 3rd Qu.:12.0 # Max. :115.0 Max. :16.0 Max. :20.0 Max. :13.0 # 인성 창의력 자격증 종합점수 # Min. : 8.0 Min. :16.0 Min. :0 Min. :65.0 # 1st Qu.: 9.0 1st Qu.:17.0 1st Qu.:0 1st Qu.:70.0 # Median :10.0 Median :18.0 Median :0 Median :72.0 # Mean : 9.4 Mean :18.2 Mean :0 Mean :71.6 # 3rd Qu.:10.0 3rd Qu.:20.0 3rd Qu.:0 3rd Qu.:75.0 # Max. :10.0 Max. :20.0 Max. :0 Max. :76.0 # 합격여부 # Length:5 # Class :character # Mode :character summary(g2) # no 가치관 전문지식 발표력 # Min. :101.0 Min. :18 Min. :13.0 Min. :14.0 # 1st Qu.:102.0 1st Qu.:18 1st Qu.:14.0 1st Qu.:15.0 # Median :104.0 Median :19 Median :15.0 Median :15.0 # Mean :105.2 Mean :19 Mean :14.4 Mean :15.6 # 3rd Qu.:106.0 3rd Qu.:20 3rd Qu.:15.0 3rd Qu.:16.0 # Max. :113.0 Max. :20 Max. :15.0 Max. :18.0 # 인성 창의력 자격증 종합점수 # Min. :12.0 Min. :10.0 Min. :1 Min. :70.0 # 1st Qu.:14.0 1st Qu.:11.0 1st Qu.:1 1st Qu.:75.0 # Median :15.0 Median :12.0 Median :1 Median :77.0 # Mean :14.8 Mean :11.8 Mean :1 Mean :75.6 # 3rd Qu.:15.0 3rd Qu.:13.0 3rd Qu.:1 3rd Qu.:77.0 # Max. :18.0 Max. :13.0 Max. :1 Max. :79.0 # 합격여부 # Length:5 # Class :character # Mode :character summary(g3) # no 가치관 전문지식 발표력 # Min. :103.0 Min. : 9 Min. :13.0 Min. :18.0 # 1st Qu.:105.0 1st Qu.:10 1st Qu.:14.0 1st Qu.:19.0 # Median :109.0 Median :11 Median :15.0 Median :20.0 # Mean :108.4 Mean :11 Mean :15.2 Mean :19.4 # 3rd Qu.:111.0 3rd Qu.:12 3rd Qu.:16.0 3rd Qu.:20.0 # Max. :114.0 Max. :13 Max. :18.0 Max. :20.0 # 인성 창의력 자격증 종합점수 # Min. : 9 Min. :5.0 Min. :0.0 Min. :57.0 # 1st Qu.:10 1st Qu.:5.0 1st Qu.:0.0 1st Qu.:61.0 # Median :11 Median :6.0 Median :0.0 Median :64.0 # Mean :11 Mean :6.2 Mean :0.4 Mean :62.8 # 3rd Qu.:12 3rd Qu.:7.0 3rd Qu.:1.0 3rd Qu.:66.0 # Max. :13 Max. :8.0 Max. :1.0 Max. :66.0 # 합격여부 # Length:5 # Class :character # Mode :character |
군집분석으로 그룹화된 군집은 다변량적 특성이 그룹 내적으로는 동일하고, 외적으로는 이질적인 특성을 갖는다.
(3) 군집 수 자르기
계층형 군집 분석 결과에서 분석자가 원하는 군집 수만큼 잘라서 인위적으로 군집을 만들 수 있다.
ex) iris 데이터 셋을 대상으로 군집 수 자르기
#1 유클리디안 거리 계산
| head(iris) # iris 데이터 보기 # Sepal.Length Sepal.Width Petal.Length Petal.Width Species # 1 5.1 3.5 1.4 0.2 setosa # 2 4.9 3.0 1.4 0.2 setosa # 3 4.7 3.2 1.3 0.2 setosa # 4 4.6 3.1 1.5 0.2 setosa # 5 5.0 3.6 1.4 0.2 setosa # 6 5.4 3.9 1.7 0.4 setosa idist <- dist(iris[1:4]) # 유클리디안 거리계산 후 계층적 군집분석 hc <- hclust(idist) hc # Call: # hclust(d = idist) # # Cluster method : complete # Distance : euclidean # Number of objects: 150 plot(hc, hang = -1) # 군집분석 시각화 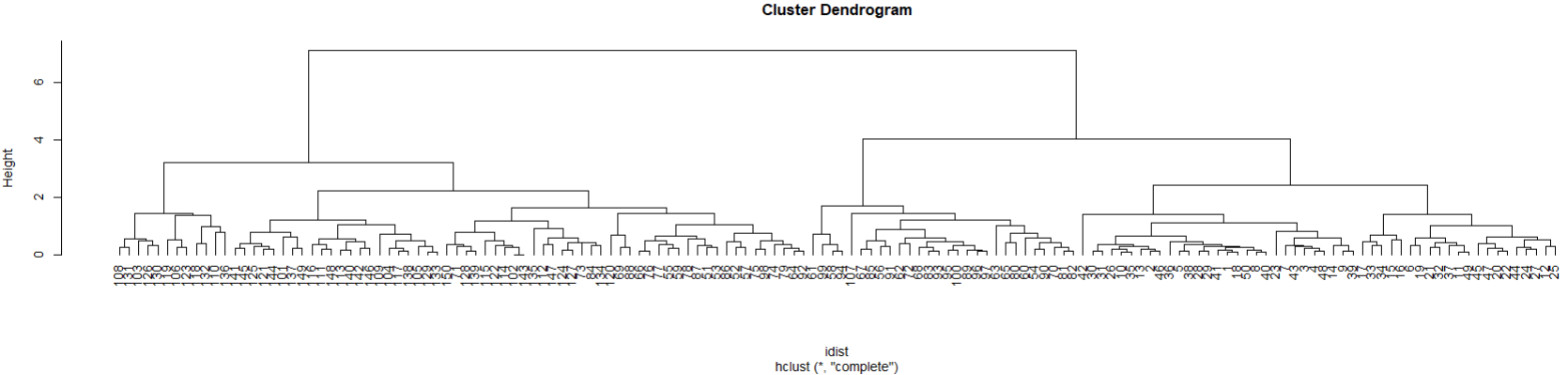 |
#2 군집 수 자르기
| ghc <- cutree(hc, k = 3) ghc # [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 # [39] 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 3 2 3 2 3 2 3 3 3 3 2 3 2 3 3 2 3 2 3 2 2 2 2 # [77] 2 2 2 3 3 3 3 2 3 2 2 2 3 3 3 2 3 3 3 3 3 2 3 3 2 2 2 2 2 2 3 2 2 2 2 2 2 2 # [115] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 |
그룹수를 자르는 함수는 stats패키지에서 제공되는 cutree()함수 이용
cutree(rPcmdwjr 군집 분석 결과, k=군집 수)
#3 iris데이터 셋에 ghc컬럼 추가
| iris$ghc <- ghc table(iris$ghc) # 1 2 3 # 50 72 28 head(iris) # Sepal.Length Sepal.Width Petal.Length Petal.Width Species ghc # 1 5.1 3.5 1.4 0.2 setosa 1 # 2 4.9 3.0 1.4 0.2 setosa 1 # 3 4.7 3.2 1.3 0.2 setosa 1 # 4 4.6 3.1 1.5 0.2 setosa 1 # 5 5.0 3.6 1.4 0.2 setosa 1 # 6 5.4 3.9 1.7 0.4 setosa 1 |
#4 요약통계량 구하기
| g1 <- subset(iris, ghc == 1) summary(g1[1:4]) # Sepal.Length Sepal.Width Petal.Length Petal.Width # Min. :4.300 Min. :2.300 Min. :1.000 Min. :0.100 # 1st Qu.:4.800 1st Qu.:3.200 1st Qu.:1.400 1st Qu.:0.200 # Median :5.000 Median :3.400 Median :1.500 Median :0.200 # Mean :5.006 Mean :3.428 Mean :1.462 Mean :0.246 # 3rd Qu.:5.200 3rd Qu.:3.675 3rd Qu.:1.575 3rd Qu.:0.300 # Max. :5.800 Max. :4.400 Max. :1.900 Max. :0.600 g2 <- subset(iris, ghc == 2) summary(g2[1:4]) # Sepal.Length Sepal.Width Petal.Length Petal.Width # Min. :5.600 Min. :2.200 Min. :4.300 Min. :1.20 # 1st Qu.:6.200 1st Qu.:2.800 1st Qu.:4.800 1st Qu.:1.50 # Median :6.400 Median :3.000 Median :5.100 Median :1.80 # Mean :6.546 Mean :2.964 Mean :5.274 Mean :1.85 # 3rd Qu.:6.800 3rd Qu.:3.125 3rd Qu.:5.700 3rd Qu.:2.10 # Max. :7.900 Max. :3.800 Max. :6.900 Max. :2.50 g3 <- subset(iris, ghc == 3) summary(g3[1:4]) # Sepal.Length Sepal.Width Petal.Length Petal.Width # Min. :4.900 Min. :2.000 Min. :3.000 Min. :1.000 # 1st Qu.:5.475 1st Qu.:2.475 1st Qu.:3.775 1st Qu.:1.075 # Median :5.600 Median :2.650 Median :4.000 Median :1.250 # Mean :5.532 Mean :2.636 Mean :3.961 Mean :1.229 # 3rd Qu.:5.700 3rd Qu.:2.825 3rd Qu.:4.200 3rd Qu.:1.300 # Max. :6.100 Max. :3.000 Max. :4.500 Max. :1.700 |
(4) 비계층적 군집 분석
군집의 수가 정해진 상태에서 군집의 중심에서 가장 가까운 개체를 하나씩 포함해 나가는 방법.
대표적인 방법이 K-means clustering
: 군집 수를 미리 알고 있는 경우 군집 대상의 분포에 따라 군집의 초기값을 설정해 주면, 초기값에서 가장 가까운 거리에 있는 대상을 하나씩 더해가는 방식.
계층적 군집 분석을 통해 대략적인 군집의 수를 파악하고 이를 초기 군집 수로 설정하여 비계층적 군집 분석을 수행하는 것이 효과적
장점: 대량의 자료를 빠르고 쉽게 분류 가능
단점: 군집의 수를 미리 알고 있어야 한다
ex) K-means 알고리즘에 군집 수를 적용하여 군집별로 시각화
#1 군집 분석에 사용할 변수 추출
| library(ggplot2) data(diamonds) # diamonds 데이터 head(diamonds) # A tibble: 6 x 10 # carat cut color clarity depth table price x y z # <dbl> <ord> <ord> <ord> <dbl> <dbl> <int> <dbl> <dbl> <dbl> # 1 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43 # 2 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31 # 3 0.23 Good E VS1 56.9 65 327 4.05 4.07 2.31 # 4 0.29 Premium I VS2 62.4 58 334 4.2 4.23 2.63 # 5 0.31 Good J SI2 63.3 58 335 4.34 4.35 2.75 # 6 0.24 Very Good J VVS2 62.8 57 336 3.94 3.96 2.48 nrow(diamonds) # 데이터 크기가 크기 때문에 아래에서 오류남 테스트 데이터 개수 지정해주기 # 53940 t <- sample(1:nrow(diamonds), 1000) # test 데이터 샘플링 t <- sample(1:nrow(diamonds), nrow(diamonds)*0.7) # test 데이터 샘플링 아래에서 result plot 실행할때 오류 test <- diamonds[t, ] dim(test) # [1] 37758 10 head(test) # A tibble: 6 x 10 # carat cut color clarity depth table price x y z # <dbl> <ord> <ord> <ord> <dbl> <dbl> <int> <dbl> <dbl> <dbl> # 1 0.28 Good F VS1 58.3 58 487 4.33 4.35 2.53 # 2 0.71 Premium F VS1 59.1 61 2839 5.84 5.81 3.44 # 3 1.39 Premium E SI2 62.7 58 7445 7.11 6.99 4.42 # 4 0.3 Very Good G VS1 62.8 58 605 4.26 4.28 2.68 # 5 0.3 Premium G SI1 62.6 57 574 4.34 4.25 2.69 # 6 0.3 Good D VS2 63.6 54 521 4.26 4.32 2.73 mydia <- test[c("price", "carat", "depth", "table")] # 문자열을 제외한 변수 추출 head(mydia) # A tibble: 6 x 4 # price carat depth table # <int> <dbl> <dbl> <dbl> # 1 487 0.28 58.3 58 # 2 2839 0.71 59.1 61 # 3 7445 1.39 62.7 58 # 4 605 0.3 62.8 58 # 5 574 0.3 62.6 57 # 6 521 0.3 63.6 54 |
t <- sample(1:nrow(diamonds), nrow(diamonds)*0.7)
result plot 실행할때 오류
# Warning messages:
# 1: In plot.window(...) : "hang"는 그래픽 매개변수가 아닙니다
# 2: In plot.xy(xy, type, ...) : "hang"는 그래픽 매개변수가 아닙니다
# 3: In axis(side = side, at = at, labels = labels, ...) :
# "hang"는 그래픽 매개변수가 아닙니다
# 4: In axis(side = side, at = at, labels = labels, ...) :
# "hang"는 그래픽 매개변수가 아닙니다
# 5: In box(...) : "hang"는 그래픽 매개변수가 아닙니다
# 6: In title(...) : "hang"는 그래픽 매개변수가 아닙니다
해결
> nrow(diamonds) 데이터 확인 하고
" t <- sample(1:nrow(diamonds), 1000) " 데이터 크기가 크기 때문에 테스트 데이터 개수 지정해주기
#2 계층적 군집 분석(탐색적 분석)
| result <- hclust(dist(mydia), method = "average") result # Call: # hclust(d = dist(mydia), method = "average") # # Cluster method : average # Distance : euclidean # Number of objects: 1000 plot(result, hang = -1)  |
#3 비계층적 군집 분석
| result2 <- kmeans(mydia, 3) names(result2) # [1] "cluster" "centers" "totss" "withinss" # [5] "tot.withinss" "betweenss" "size" "iter" # [9] "ifault" result2$cluster mydia$cluster <- result2$cluster head(mydia) # A tibble: 6 x 5 # price carat depth table cluster # <int> <dbl> <dbl> <dbl> <int> # 1 353 0.31 59.4 62 1 # 2 8333 1 62.2 55 2 # 3 878 0.3 62.7 57 1 # 4 1927 0.72 60.7 60 1 # 5 10910 1.7 62.4 58 3 # 6 1685 0.54 60.8 62 1 |
kmeans()함수
#4 변수 간의 상관계수 보기
| cor(mydia[ , -5], method = "pearson") # price carat depth table # price 1.000000000 0.91027770 -0.002135156 0.05318351 # carat 0.910277698 1.00000000 0.077611992 0.08606998 # depth -0.002135156 0.07761199 1.000000000 -0.29397756 # table 0.053183511 0.08606998 -0.293977565 1.00000000 plot(mydia[ , -5]) 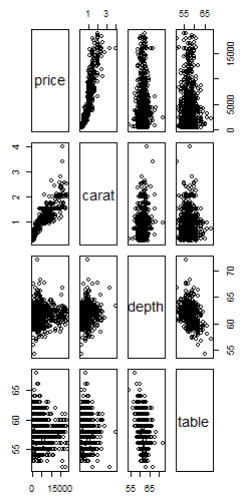 |
cor()함수
#5 상관계수를 색상으로 시각화
| install.packages("mclust") library(mclust) install.packages("corrgram") library(corrgram) corrgram(mydia[ , -5], upper.panel = panel.conf)  corrgram(mydia[ , -5], lower.panel = panel.conf)  |
corrgram()함수
#6 비계층적 군집 시각화
plot(mydia$carat, mydia$price, col = mydia$cluster)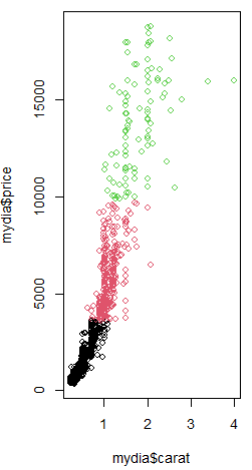 points(result2$centers[ , c("carat", "price")],col = c(3, 1, 2), pch = 8, cex = 5) 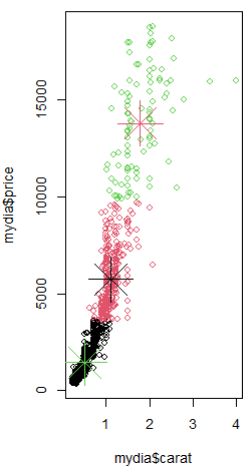 |
corrgram()함수
'통계기반 데이터분석' 카테고리의 다른 글
| [ R ] 연관분석 #2 시각화 (0) | 2022.12.04 |
|---|---|
| [ R ] 연관분석 #1 (0) | 2022.12.04 |
| [ R ] 군집분석 #1 (0) | 2022.12.03 |
| [ R ] 오분류표 (1) | 2022.12.03 |
| [ R ] 변수제거 (1) | 2022.12.03 |


