59doit
[ R ] 주요 내장함수 본문
반응형
주요 내장함수
(1) 기술통계량 처리 관련 내장함수
- min(vec), max(vec), range(vec), mean(vec), median(vec), sum(vec), sort(x), order(x): 벡터의 정렬된 값의 index를 보여주는 함수
- rank(x), sd(x), summary(x), table(x), sample(x,y): x범위에서 y만큼 sample데이터를 생성하는 함수
ex ) 행/컬럼 단위의 합계와 평균 구하기
| library(RSADBE) data("Bug_Metrics_Software") Bug_Metrics_Software[ , , 1] # Bugs # Software Bugs NT.Bugs Major Critical H.Priority # JDT 11605 10119 1135 432 459 # PDE 5803 4191 362 100 96 # Equinox 325 1393 156 71 14 # Lucene 1714 1714 0 0 0 # Mylyn 14577 6806 592 235 8804 |
#1 행 단위 합계와 평균 구하기
| rowSums(Bug_Metrics_Software[,,1]) # JDT PDE Equinox Lucene Mylyn # 23750 10552 1959 3428 31014 rowMeans(Bug_Metrics_Software[,,1]) # JDT PDE Equinox Lucene Mylyn # 4750.0 2110.4 391.8 685.6 6202.8 |
#\2 열 단위 합계와 평균 구하기
| colSums(Bug_Metrics_Software[ , , 1]) # Bugs NT.Bugs Major Critical H.Priority # 34024 24223 2245 838 9373 colMeans(Bug_Metrics_Software[ , , 1]) # Bugs NT.Bugs Major Critical H.Priority # 6804.8 4844.6 449.0 167.6 1874.6 |
- rowSums()함수: 행 단위 합계
- rowMeans()함수: 행단위 평균
- colSums()함수: 열 단위 합계
- colMeans()함수: 열 단위 평균
ex ) 기술통계량 관련 내장함수 사용하기
| seq(-2, 2, by = .2) # [1] -2.0 -1.8 -1.6 -1.4 -1.2 -1.0 -0.8 -0.6 -0.4 -0.2 0.0 0.2 0.4 # [14] 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0 vec <- 1:10 min(vec) # [1] 1 max(vec) # [1] 10 range(vec) # [1] 1 10 mean(vec) # [1] 5.5 median(vec) # [1] 5.5 sum(vec) # [1] 55 sd(rnorm(10)) # [1] 1.106399 table(vec) # vec # 1 2 3 4 5 6 7 8 9 10 # 1 1 1 1 1 1 1 1 1 1 |
ex ) 정규분포의 난수 생성
| n <- 1000 rnorm(n, mean = 0, sd = 1) # [1] -1.5819162794 -1.4636645806 0.6356763391 -0.6909254936 # [5] 0.1827160398 0.3247198464 1.3189940544 0.4820108120 # [9] -0.3504090516 -0.7553309475 1.7931453812 -0.0846528568 # ... # [989] -1.0200738335 -1.2600623873 -0.6815866979 0.6193155104 # [993] -1.1114083366 0.5968691113 -0.4569059239 0.5785676314 # [997] -0.6087455611 1.5691507395 -1.6128050872 0.5541534259 hist(rnorm(n, mean = 0, sd = 1)) 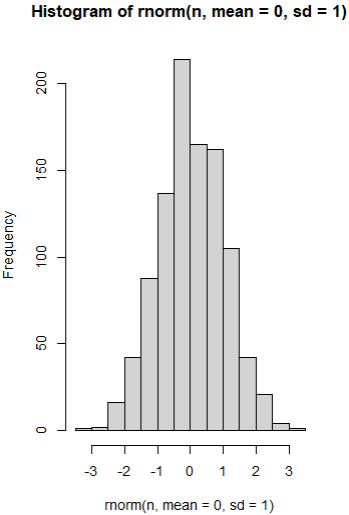 |
- rnorm()함수: rnorm(n, mean, sd) #평균과 표준편차 이용
ex ) 균등분포의 난수 생성하기
n <- 1000 runif(n, min = 0, max = 10) # [1] 8.7372130156 9.9497853452 5.9499506280 4.3300856370 # [5] 2.6185516058 1.8008810724 7.3364510643 8.5163394222 # [9] 0.3423158615 3.8630999438 7.6968584303 7.6367642009 # ... # [989] 9.3462432572 4.5198559482 9.1954133334 0.2619184717 # [993] 8.6162055982 2.8446740727 4.6599535085 2.5132839591 # [997] 4.7290140647 7.9416073067 4.5055965125 5.3943388537 hist(runif(n, min = 0, max = 10))  |
- runif(n, min, max) #최소값, 최대값 이용
ex ) 이항분포의 난수 생성하기
| n <- 20 rbinom(n, 1, prob = 1 /2 ) # [1] 0 1 0 0 1 1 1 1 0 0 1 1 1 0 0 1 1 0 0 1 rbinom(n, 2, 0.5) # [1] 1 0 1 1 2 1 0 2 1 1 0 1 1 1 0 2 2 2 1 1 rbinom(n, 10, 0.5) # [1] 3 5 5 3 5 5 6 7 5 6 4 7 4 3 8 5 5 7 3 6 n <- 1000 rbinom(n, 5, prob = 1 / 6) # [1] 0 2 0 1 0 1 0 0 1 1 1 1 0 0 1 0 0 1 2 1 1 1 0 1 1 1 # [27] 1 1 0 0 0 1 2 2 0 1 0 0 1 2 1 0 0 2 0 1 1 0 1 2 2 1 # .... ... |
- rbinom(n, size, prob) #독립적 n의 반복
ex ) 종자값으로 동일한 난수 생성
- 종자(seed)값을 지정하면 동일한 난수 발생 가능
- 종자(seed)값 지정을 위해 seed()함수 사용
- set.seed(임의의 정수) #임의의 정수를 종자값으로 하여 동일한 난수 생성
| rnorm(5, mean = 0, sd = 1) set.seed(123) rnorm(5, mean = 0, sd = 1) set.seed(123) rnorm(5, mean = 0, sd = 1) set.seed(345) rnorm(5, mean = 0, sd = 1) |
(2) 수학 관련 내장함수
- abs(x), sqrt(x), ceiling(x), floor(), round(), factorial(x), which.min(x), which.max(x): 벡터 내 최소값과 최대값의 인덱스를 구하는 함수
- pmin(x, pmax(x): 여러 벡터에서의 원소 단위 최소값과 최대값을 구하는 함수
- Prod(): 곱 cumsum(), cumprod(), cos(x), sin(x), tan(x), log(x), log10(x), exp(x)
ex ) 수학 관련 내장함수 사용
(3) 행렬연산 관련 내장함수
- 행렬 분해(matrix decomposition)는 행렬을 특정한 구조를 가진 다른 행렬의 곱으로 나타내는 것
- eigen(), svd(), qr(), chol()
- ncol(x), nrow(x), t(x), cbind(…), rbind(…), diag(x), det(x), appply(x, m, fun), solve(x): 역행렬
- eigen(x): 정방행렬을 대상으로 고유값 분해하는 함수
- svd(x): mxn 행렬을 대상으로 특이값을 분해하는 함수
- x%*%y: 두 행렬의 곱을 구하는 수식
ex ) 행렬연산 내장함수 사용하기
| x <- matrix(1:9, nrow = 3, ncol = 3, byrow = T) y <- matrix(1:3, nrow = 3) ncol(x) # [1] 3 nrow(x) # [1] 3 t(x) # [,1] [,2] [,3] # [1,] 1 4 7 # [2,] 2 5 8 # [3,] 3 6 9 cbind(x, 1:3) # [,1] [,2] [,3] [,4] # [1,] 1 2 3 1 # [2,] 4 5 6 2 # [3,] 7 8 9 3 rbind(x, 10:12) # [,1] [,2] [,3] # [1,] 1 2 3 # [2,] 4 5 6 # [3,] 7 8 9 # [4,] 10 11 12 diag(x) # [1] 1 5 9 det(x) # [1] 6.661338e-16 apply(x, 1, sum) # [1] 6 15 24 apply(x, 2, mean) # [1] 4 5 6 svd(x) # $d # [1] 1.684810e+01 1.068370e+00 4.418425e-16 # # $u # [,1] [,2] [,3] # [1,] -0.2148372 0.8872307 0.4082483 # [2,] -0.5205874 0.2496440 -0.8164966 # [3,] -0.8263375 -0.3879428 0.4082483 # # $v # [,1] [,2] [,3] # [1,] -0.4796712 -0.77669099 -0.4082483 # [2,] -0.5723678 -0.07568647 0.8164966 # [3,] -0.6650644 0.62531805 -0.4082483 eigen(x) # eigen() decomposition # $values # [1] 1.611684e+01 -1.116844e+00 -1.303678e-15 # # $vectors # [,1] [,2] [,3] # [1,] -0.2319707 -0.78583024 0.4082483 # [2,] -0.5253221 -0.08675134 -0.8164966 # [3,] -0.8186735 0.61232756 0.4082483 x %*% y # [,1] # [1,] 14 # [2,] 32 # [3,] 50 |
(3) 집합연산 관련 내장함수
- 집합을 대상으로 합집합, 교집합, 차집합 등의 집합연산을 수행하는 R의 내장함수
- union(x,y), setequal(x,y), intersect(x,y), setdiff(x,y), c%in%y
%any%특별연산자
ex ) %% 나머지 연산자 : a %% b
- a를 b로 나눈 나머지
| x <-c(1,2,3,4,5) y <-c(5) x %% y # [1] 1 2 3 4 0 |
ex ) %*% 연산자 : a %*% b
- 연산자는 a와 b를 곱한다
| x <- matrix(c(1, 4, 2, 3), nrow = 2) x # [,1] [,2] # [1,] 1 2 # [2,] 4 3 y <- matrix(c(1, 3, 2, 4, 5, 6), nrow = 2) y # [,1] [,2] [,3] # [1,] 1 2 5 # [2,] 3 4 6 |
#1 2행 2열인 Matrix와 2행 3열인 Matrix를 곱하기 연산을 한다
| x%*%y z <- matrix(c(1, 2, 3, 4, 5, 6, 7, 8, 9), nrow = 3) z # [,1] [,2] [,3] # [1,] 1 4 7 # [2,] 2 5 8 # [3,] 3 6 9 |
#2 Error ; 2행 2열인 Matrix와 3행 3열인 Matrix를 곱하기 연산을 하면 오류가 발생한다.
| x%*%z # non-conformable arguments |
#3 2행 3열인 Matrix와 3행 3열인 Matrix를 곱하기 연산을 한다.
| y%*%z # [,1] [,2] [,3] # [1,] 20 44 68 # [2,] 29 68 107 |
#4 2행 3열인 Matrix와 3행 3열인 Matrix를 곱하기 연산을 한다.
| c(1, 2, 3) %*% c(4, 5, 6) # [,1] # [1,] 32 |
ex ) %/% 연산자 : a %% b ;
- a %/% b A를 b로 나눈다.
- 요소별로 연산한다.
- %/% 연산자로 나눈 결과에서 소수점은 절삭을 하여 반환한다.
| x <- matrix(c(1, 4, 2, 3), nrow = 2) x # [,1] [,2] # [1,] 1 2 # [2,] 4 3 y <- matrix(c(1, 3, 2, 4), nrow = 2) y # [,1] [,2] # [1,] 1 2 # [2,] 3 4 |
#1 나누기 연산을 한다
| x %/% y # [,1] [,2] # [1,] 1 1 # [2,] 1 0 z <- matrix(c(1, 2, 3, 4, 5, 6, 7, 8, 9), nrow = 3) # [,1] [,2] [,3] # [1,] 1 4 7 # [2,] 2 5 8 # [3,] 3 6 9 |
#2 Error 크기가 맞지 않아 오류가 발생한다.
| x %/% z # non-conformable arguments |
ex )벡터 내 특정 값 포함 여부 확인 연산자 %in% :a %in% b
- 벡터 내 특정값이 포함되었는지 여부 확인
- TRUE, FALSE 논리형 벡터 출력
| x %in% y [1] TRUE TRUE TRUE TRUE sum(x %in% y) [1] 1 |
반응형
'Programming > R' 카테고리의 다른 글
| [ R ] dplyr 패키지 활용 #2 (0) | 2022.11.19 |
|---|---|
| [ R ] dplyr 패키지 활용 #1 (0) | 2022.11.19 |
| [ R ] 함수의 정의 (0) | 2022.11.18 |
| [ R ] 연산자 & 조건문 & 반복문 (0) | 2022.11.17 |
| [ R ] 연습문제 (3) (0) | 2022.11.17 |
Comments
